Cálculo de Varianza en Excel: Una Guía con Ejemplos
La varianza es una medida estadística que nos indica cuánto están dispersos un conjunto de números. Es un concepto crucial en las finanzas, la ciencia y muchos otros campos, ayudándonos a comprender la variabilidad o dispersión dentro de nuestros conjuntos de datos. Excel proporciona una manera sencilla de calcular la varianza, lo que la hace accesible tanto para principiantes como para usuarios avanzados. En este artículo, exploraremos cómo hacerlo con ejemplos claros.
¿Qué es la varianza?
Introducción a las funciones de varianza en Excel
¿Cómo calcular la varianza en Excel?
- VAR.S vs VAR.P – Calcular la varianza desde una muestra o población
- VAR.S vs VARA – Calcular la varianza incluyendo o excluyendo textos y valores lógicos
Varianza vs Desviación estándar
¿Qué es la varianza?
La varianza es un término estadístico que describe el grado en que los números de un conjunto de datos difieren de la media, o promedio, de esos números. Básicamente, mide qué tan dispersos están los números. Un punto clave para entender la varianza es reconocer que cuantifica el grado de variación o dispersión dentro de un conjunto de valores. Una alta varianza indica que los números están muy dispersos; una baja varianza sugiere que están agrupados cerca de la media.
Un ejemplo sencillo para ilustrar la varianza:
Escenario: Consideremos una clase con cinco estudiantes y sus calificaciones en un examen de matemáticas sobre 100. Las puntuaciones son 90, 92, 88, 91 y 89.
Calcular la Media: Primero, encontramos la calificación promedio (media). La media es
Calcular la Varianza: Luego, calculamos la varianza. Esto implica restar la media de cada puntuación, elevar al cuadrado el resultado y luego promediar estas diferencias al cuadrado.
= [0 + 4 + 4 + 1 + 1] / 5
= 10 / 5
= 2
Un gráfico mostró la dispersión de las puntuaciones:
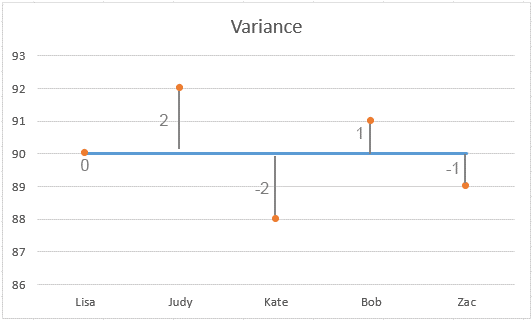
Comprender el Resultado:
Baja Varianza: En este ejemplo, la varianza es 2. Esto es relativamente bajo, lo que indica que la mayoría de las puntuaciones están cerca de la media (90). Cuanto menor sea la varianza, más cerca estarán los números individuales del conjunto respecto a la media.
Varianza Cero: Si todos los estudiantes hubieran obtenido exactamente 90, la varianza sería 0, indicando que no hay variabilidad en absoluto. Todas las puntuaciones serían iguales.
Alta Varianza: Por el contrario, una varianza más alta indicaría que las puntuaciones están más dispersas respecto a la media, mostrando una mayor variabilidad en el rendimiento de los estudiantes.
En resumen, la varianza nos da un valor numérico que ayuda a cuantificar cuánto se desvían las puntuaciones (o cualquier conjunto de números) del valor promedio, proporcionando información sobre la consistencia o variabilidad de los datos.
Introducción a las funciones de varianza en Excel
Excel proporciona varias funciones para calcular la varianza, cada una diseñada para diferentes escenarios de datos.
Comprender estas funciones es crucial para un análisis estadístico preciso.
VAR.S (Varianza de Muestra, solo incluyendo números):
- Calcula la varianza basada en una muestra de una población.
- Es mejor usarla cuando se analiza un subconjunto de datos para inferir sobre el total.
VAR.P (Varianza de Población, solo incluyendo números):
- Calcula la varianza para toda la población.
- Ideal cuando tienes datos completos y no solo una muestra.
VARA (Varianza de Muestra, incluyendo texto y valores lógicos):
- Similar a VAR.S pero incluye texto y valores lógicos en el cálculo (el texto se trata como 0, VERDADERO como 1, FALSO como 0).
- Útil cuando tu conjunto de datos contiene tipos mixtos (números, texto y valores lógicos).
VARPA (Varianza de Población, incluyendo texto y valores lógicos):
- La versión de varianza de población de VARA.
- Incluye todos los tipos de datos en el cálculo de la varianza para toda la población.
VAR (Varianza de Muestra Legado):
- Una versión anterior de VAR.S, utilizada principalmente en Excel 2007 y versiones anteriores.
- Se recomienda usar VAR.S en versiones más recientes para mayor consistencia y claridad.
VARP (Varianza de Población Legado):
- La versión anterior de VAR.P.
- Al igual que VAR, se recomienda usar VAR.P en versiones más nuevas de Excel.
Diferencias y Comparaciones:
- Muestra vs. Población: VAR.S y VARA son para muestras, mientras que VAR.P y VARPA son para toda la población.
- Consideración de Tipo de Datos: VARA y VARPA incluyen texto y valores lógicos en el cálculo, a diferencia de VAR.S y VAR.P.
- Funciones Antiguas vs. Modernas: VAR y VARP son funciones antiguas y pueden ser reemplazadas por VAR.S y VAR.P para una mejor compatibilidad con las versiones actuales de Excel.
Tabla de Comparación:
| Función | Tipo de Datos Considerados | Población o Muestra | Caso de Uso |
| VAR.S | Solo Números | Muestra | Varianza de muestra para datos numéricos |
| VAR.P | Solo Números | Población | Varianza de población para números |
| VARA | Números, Texto, Valores Lógicos | Muestra | Varianza de muestra para datos mixtos |
| VARPA | Números, Texto, Valores Lógicos | Población | Varianza de población para datos mixtos |
| VAR | Solo Números | Muestra | Función legado para varianza de muestra |
| VARP | Solo Números | Población | Función legado para población |

Descubre la Magia de Excel con Kutools AI
- Ejecución Inteligente: Realiza operaciones en celdas, analiza datos y crea gráficos, todo impulsado por comandos simples.
- Fórmulas Personalizadas: Genera fórmulas adaptadas para optimizar tus flujos de trabajo.
- Codificación VBA: Escribe e implementa código VBA sin esfuerzo.
- Interpretación de Fórmulas: Comprende fórmulas complejas con facilidad.
- Traducción de Texto: Supera las barreras del idioma dentro de tus hojas de cálculo.
¿Cómo calcular la varianza en Excel?
En esta sección, proporcionaremos dos ejemplos para demostrar cómo calcular la varianza en Excel y explicaremos las diferencias entre las diversas funciones de varianza. Como resultado, verás que diferentes funciones de varianza producen resultados completamente diferentes para los mismos datos de ejemplo.
VAR.S vs VAR.P – Calcular la varianza desde una muestra o población
Escenario: Calcular la varianza para una pequeña muestra de una población frente a toda la población.
Ejemplo: Calcula la varianza para los valores en la columna A2:A12.
Fórmula: Selecciona una celda en blanco y escribe una de las siguientes fórmulas según sea necesario, luego presiona la tecla Enter.
Obtener las varianzas para la muestra de un gran conjunto de datos (suponiendo que los valores en A2:A12 son partes de un gran conjunto de datos)
=VAR.S(A2:A12)
Obtener la varianza para toda la población (suponiendo que los valores en A2:A12 son todo el conjunto de datos)
=VAR.P(A2:A12)
Como ves, los mismos valores pero usando diferentes funciones de varianza darán resultados diferentes.
¿Por qué los resultados de VAR.S y VAR.P son diferentes?
- VAR.S: Esta función se utiliza cuando tu conjunto de datos representa una muestra de una población más grande. Calcula la varianza basada en el método "n-1", donde "n" es el número de puntos de datos en la muestra. Usar "n-1" en lugar de "n" como denominador corrige el sesgo en la muestra, convirtiéndola en un estimador insesgado de la varianza de la población. Proporciona una estimación de cómo los datos en la muestra varían alrededor de la media de la muestra.
- VAR.P: Esta función se utiliza cuando tu conjunto de datos representa una población completa, no solo una muestra de ella. Calcula la varianza basada en el método "n", donde "n" es el número de puntos de datos en la población. Asume que el conjunto de datos cubre toda la población, por lo que no es necesario corregir el sesgo como en VAR.S.
- En resumen, la diferencia clave está en el denominador de la fórmula. VAR.S usa "n-1" para tener en cuenta la naturaleza muestral de los datos, mientras que VAR.P usa "n" para datos poblacionales donde no hay muestreo involucrado. Dependiendo de tu conjunto de datos y si es una muestra o una población completa, debes elegir la función adecuada para calcular la varianza.
VAR.S vs VARA – Calcular la varianza incluyendo o excluyendo textos y valores lógicos
Escenario: Decidir si incluir valores lógicos y textos en el cálculo de la varianza.
Ejemplo: Calcula la varianza para los valores en la columna A2:A12.
Fórmula: Selecciona una celda en blanco y escribe una de las siguientes fórmulas según sea necesario, luego presiona la tecla Enter.
Obtener las varianzas para la muestra de un gran conjunto de datos ignorando textos y valores lógicos.
=VAR.S(A2:A12)
Obtener la varianza para la muestra de un gran conjunto de datos incluyendo textos y valores lógicos.
=VARA(A2:A12)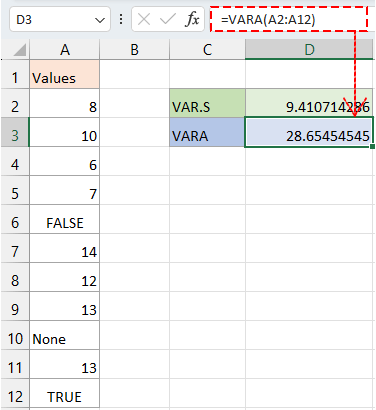
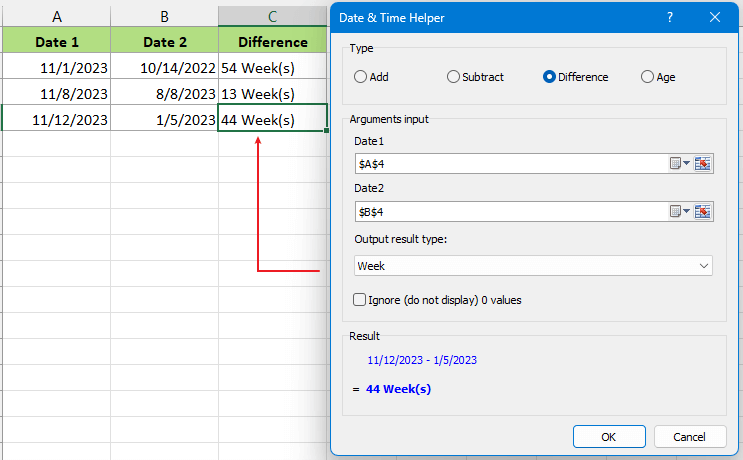
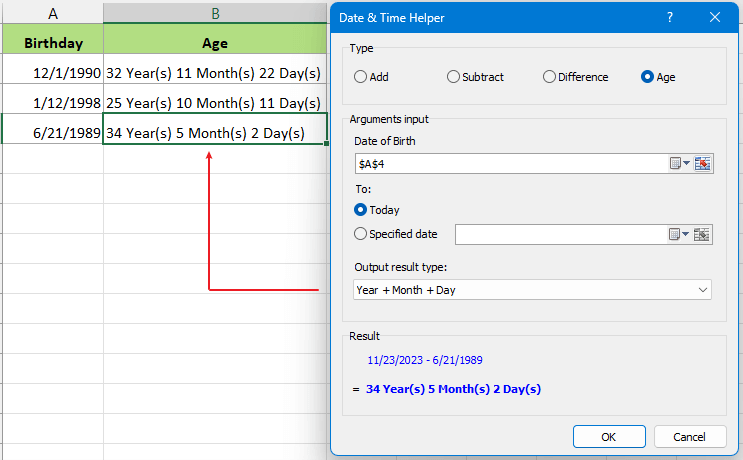
Hacer volar los cálculos de fecha y hora
El Asistente de Fecha y Hora de Kutools para Excel es una herramienta increíblemente eficiente diseñada para simplificar cálculos complejos de fecha y hora. Pruébalo y descubre cómo transforma tu experiencia de gestión de datos.
Varianza vs Desviación estándar
Similitudes:
Medida de Dispersión:
Tanto la varianza como la desviación estándar son medidas estadísticas utilizadas para describir la dispersión o variabilidad dentro de un conjunto de datos. Cuantifican qué tan lejos están los números individuales del conjunto respecto a la media (promedio).
Análisis de Datos:
Ambas se usan comúnmente en el análisis estadístico para comprender la variabilidad de los datos. Son esenciales en campos como las finanzas, la investigación, el control de calidad y más.
Calculadas a partir de la Media:
El cálculo tanto de la varianza como de la desviación estándar comienza con la media del conjunto de datos. Evalúan la variabilidad en relación con este valor central.
Diferencias:
Unidades de Medida:
Varianza: Unidades al cuadrado de los datos originales. Por ejemplo, si los datos están en metros, la varianza estará en metros cuadrados.
Desviación Estándar: Mismas unidades que los datos originales. Continuando con el ejemplo, si los datos están en metros, la desviación estándar también estará en metros.
Interpretación:
Varianza: Proporciona una estimación al cuadrado que puede ser menos intuitiva de interpretar porque no está en la misma escala que los datos originales.
Desviación Estándar: Más interpretable ya que está en las mismas unidades que los datos. Indica la distancia promedio de los puntos de datos respecto a la media.
Definición Matemática:
Varianza: El promedio de las diferencias al cuadrado respecto a la Media.
Desviación Estándar: La raíz cuadrada de la varianza.
Sensibilidad a Valores Extremos:
Varianza: Más sensible a valores atípicos porque eleva al cuadrado las diferencias.
Desviación Estándar: Aunque afectada por valores atípicos, es menos sensible en comparación con la varianza debido a la raíz cuadrada.
Aplicaciones:
Varianza:
Se utiliza cuando el enfoque está en la magnitud al cuadrado de la dispersión.
Beneficiosa en modelos y cálculos estadísticos donde elevar al cuadrado es necesario para anular valores negativos.
Usualmente empleada en modelos financieros para la evaluación de riesgos, ya que mide la volatilidad.
Desviación Estándar:
Más comúnmente usada en informes y aplicaciones diarias debido a su relación directa con la escala de los datos.
Esencial en investigaciones empíricas para comprender la variabilidad.
Usualmente empleada en control de calidad, informes meteorológicos y puntuaciones estándar en pruebas.
Conclusión:
Si bien tanto la varianza como la desviación estándar sirven para medir la dispersión de un conjunto de datos, sus aplicaciones difieren debido a su unidad de medida e interpretabilidad. La desviación estándar, con su relación directa con la escala de los datos, tiende a ser más fácil de usar, especialmente en contextos prácticos y cotidianos. La varianza, por otro lado, suele ser más adecuada para modelos matemáticos y estadísticos.
Esta visión general y comparación debería proporcionar una comprensión clara de cuándo y por qué usar cada función de varianza en Excel, permitiendo un análisis de datos más preciso y significativo. Para más estrategias revolucionarias de Excel que pueden elevar tu gestión de datos, explora más aquí.
Las Mejores Herramientas de Productividad para Office
Kutools para Excel - Te Ayuda a Sobresalir de la Multitud
Kutools para Excel cuenta con más de 300 funciones, asegurando que lo que necesitas esté a solo un clic de distancia...
Office Tab - Habilita la Lectura y Edición con Pestañas en Microsoft Office (incluye Excel)
- ¡Un segundo para cambiar entre docenas de documentos abiertos!
- Reduce cientos de clics del ratón para ti cada día, di adiós al síndrome del túnel carpiano.
- Aumenta tu productividad en un 50% al ver y editar múltiples documentos.
- Trae pestañas eficientes a Office (incluye Excel), igual que Chrome, Edge y Firefox.
Tabla de contenido
- ¿Qué es la varianza?
- Introducción a las funciones de varianza en Excel
- ¿Cómo calcular la varianza en Excel?
- VAR.S vs VAR.P – Calcular la varianza desde una muestra o población
- VAR.S vs VARA – Calcular la varianza incluyendo o excluyendo textos y valores lógicos
- Varianza vs Desviación estándar
- Artículos Relacionados
- Las Mejores Herramientas de Productividad para Office
- Comentarios